Teaching Math With Manipulatives

Understanding, not "knowing all the facts," is the key to educational success.

The possession of facts, mere "information," is insufficient as an end to Education. That's what we have computers for.

We demand understanding from our students.
But what counts as understanding?
How do we know it when we see it?
Does it have something to do with concepts, forming concepts, having a concept of something, what?
To use a concept to perform a task shows familiarity with a concept.
A monkey may use a handy stick to reach a banana and feed itself.
An octopus may learn, from seeing it done by another octopus, how to open a jar to get food.
But to verbalize a concept is to demonstrate the highest form of understanding.

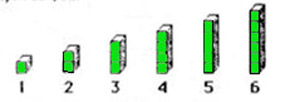
A primitive man may employ a handy stave as a lever to flip a log.

An engineer can tell you how long a lever would be necessary for a man of one hundred kilos to flip the Queen Mary.

This entails being able to distinguish it from other similar concepts, to show how it is related to similar concepts, and being able to say what is necessary and sufficient for the concept to exist and to function. These are not things you memorize.

To distinguish a concept is to apply the "principle of distinctness" and to apply the "law of the excluded middle." A thing is either this thing, or that thing, if we cannot distinguish an object from another object they are the same object, (or kind of object, if multiples are permissible.)

Then one must show the "necessary and sufficient conditions" and finally to show how it "relates" to the existing conceptual framework in which it is to be found "meaningful." But this last step we might leave until post-secondary education. heh.

Do all that and you will have achieved "understanding."

Is anything less, acceptable?

Number concept and Multiplication facts.

If a child can recite all the numbers from one to ten in sequence, is this proof of the understanding of magnitude? Does she know that 4 is bigger than 3? Just because it comes later in the sequence doesn't automatically imply that a thing is somehow "bigger" than its predecessor. If that were true, children would imagine that the letter "Z" was twenty-six times bigger than the letter "A."

No, the concept of "increase in size with the procession of terms" must be taught, or better yet, learned.

But how?

If all that a child sees in her mind's eye, when the number names are recited to her, is a string of Arabic symbols, as in: 1,2,3,4,5,6,7,8,9, then increase in magnitude must be taught separately.

However, if, as a number name is presented, say "three," a block, of three cubes stuck together say, was presented, or a drawing of same, and "3" was used as the "name of the thing" presented, then we followed this with 2 as a block of two units stuck together, the student can readily appreciate first hand that 3 is larger than 2 sensorily - by sight and by touch.

Piaget called this sensori-motor experience, a schema or pre-concept.

With further relevant experiences the concept is formed as the essence of the concept is synthesized by the cognitive processes inherent in the human mind. Piaget called these the processes of assimilation and accommodation. This is learning.

As the learning experience proceeds, the child typically begins to apply the acquired experiences in a variety of spontaneous experiments called "play." We call the process "explore and discover."

In the extreme case of yesteryear, a student could be drilled in times tables until perfect response is elicited by a command of "7 times 6 equals?" but it is entirely possible that the child may not know that "forty-two" consists of four tens and two units, or is also twice 21. Just as a perfect response of "saves nine!" can be trained to the prompt, "A stitch in time?" or more insidiously,

"Veni, vidi?" can get a response of "vici!" and the respondent need have no more comprehension of Latin than one of Pavlov's dogs. If the example were from Homer the analogy would be complete, for reciting times tables correctly need have no more significance to the pupil than Greek poetry, she might easily respond when asked, "What does 7 times 6 mean?" by saying, I dunno, it's as Greek to me!"

But let's go further, if the algorithm for two or three digit multiplication were trained by form and practice. Each step being a result taken from a suitable times table, if recorded correctly, a student could do the sum 54 times 872, find the answer 47188, and have no idea why it works, whether that is the right answer or if it is wrong by a hundred! This complicated action has been performed by hundreds of millions of schoolchildren around the world for more than a hundred years, I wouldn't test anybody's credulity by claiming here and now that literally millions of those students had no idea what it meant, or even whether or not they got it right, much less "understood" it.

You see, understanding was never the goal, performance was. All that mattered was whether or not you got it right on the test.

Before the Second World War, a "computer" was a valued job in the military held by somebody who was good at arithmetic with a pencil and paper. A computer was someone who could calculate trajectories for artillery, quickly and accurately. They didn't have electronic machines to do that back then. They trained these personnel by drill, under great pressure, until they could be relied upon to give the right answers while shells were exploding around them and they were under fear of death. School exams are a little better now.

Understanding is the key to extending motivation beyond tenth grade.

As discipline has eroded due to the abolishing of the traditional means of instilling it, to wit, the cane, the strap, the slipper and other forms of corporal punishment, useless essays and writing of lines as punishment, and detentions are banished because of busing, even verbal thrashings are frowned upon. Without the means of enforcing the discipline, methods dependent on drill and practice, are doomed to fail. Kids would rather play baseball than practice times tables.

Therefore, if you want interest in mathematics to persist beyond grade ten - the time when math becomes optional in many schools, then you need a method that does not depend on short-term memorization of facts, rules, formulae and processes for its success.

The best alternative to "drilling," is understanding.

Why?

Because understanding a concept is usually accompanied by the production of dopamine and endorphins in the brain, in short, pleasure. When that little light goes on, and you finally "get it," it feels good!

Jean Piaget and Maria Montessori have shown that understanding of concepts occurs naturally in children if the appropriate sensori-motor experiences can be had. That means the necessary opportunity for exploring and discovering concepts must be provided for the children to learn naturally; in other words, play.

But not just any play, if you want children to learn language you must provide a language-rich environment. If you want children to learn math concepts you must provide a math-rich environment. More on that later, let's get this straight: sensori-motor experiences of the right kind are necessary for the acquisition of schemas - groups of experiences, that can be assimilated and synthesized into concepts or accommodated by the child's mind. This sense of understanding is enjoyable and is all that is needed for successful learning.

It is our mission as teachers and parents to provide the appropriate materials and situations for this to happen, and sometimes just to get out of the way.

While that made me happy, by 1998 the demand on my schedule had become so heavy I knew had to find another way to reach more people. My solution was to record my workshop on video. I willingly sent the tapes to interested parties I couldn't teach in person. The problem with that scheduling solution was no one could ask questions. Extra explanations were missing because I wasn't there in person at the white board. That led me to the development of a handbook.

I'll tell you more about that in a minute. You probably want to know more about the Mortensen Math system first.

MORTENSON MORE THAN MATH employs manipulatives to enhance the child's ability to visualize math concepts, to decode the mathematical language into spatial reality.

The best way I know to explain the Mortensen Math system is to talk about memory first. How good is your short-term memory? More importantly, how good is your short-term memory with numbers? Suppose I gave you 12 numbers, each of them seven digits long. Do you think you could remember them for an hour? Five minutes? Do you think you could remember them long enough to write them down, even right after I told you?

Not likely. That's because you've been taught like everyone else to memorize the hard way. The hard way is how most students are taught math as well.

The truth is the entire math curriculum used in traditional teaching situations, employing textbooks, relies on memorizing nothing but FACTS, RULES, FORMULAE AND PROCESS!

Our job as educators is to decode this mathematical language of symbols into a concrete reality. This is what the method does. For a free sample, a 20 page .pdf of how to teach multiplication with manipulatives, go to the main page and click upper right where it says FREE eBook.